Digitale Filter und Filterstrukturen

Digitale Filter können in Form von Differenzengleichungen dargestellt werden. Hierbei gibt es sowohl einen nicht-rekursiven als auch einen rekursiven Teil. Der rekursive Teil bezieht sich auf vorherige Ausgangssignale, während der nicht-rekursive Teil sich lediglich auf das Eingangssignal bezieht.

Wenn wir die Differenzengleichung nach $a_{0} = 1$ normalisiert darstellen, können wir das Ausgangssignal auf die eine Seite und alles andere auf die andere Seite stellen. Wir erhalten somit:

Im Folgenden verwenden wir jedoch diese Form zur Diskussion von digitalen Filter- und Filterstrukturen. Einige Programme jedoch verwenden die erste. Eine Umrechnung muss somit bedacht werden.

1. Darstellung Im Blockdiagramm

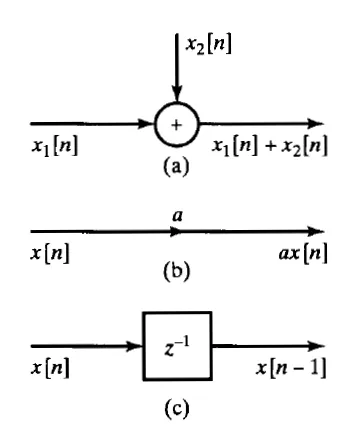
Fälschungsstrukturen können in einem Blockdiagramm dargestellt werden. Hierfür vereinbaren wir folgende Symbole und Darstellungen. Das erste Beispiel zeigt eine Addition von einem Eingangssignal x1 und x2. Das zweite Beispiel zeigt eine Multiplikation mit einem Skalarfaktor. Und das dritte Beispiel zeigt eine Verzögerung um 1.

Nicht-rekursive Filter mit endlicher Impulsantwort nennt man FIR-Filter.

Und rekursive Filter mit in der Regel unendlicher Impulsantwort nennt man IIR-Filter.